09/07/2021

Limit of Functions

Now we're going to review the limit of a function and see some examples. First of all, let's recall the rigorous definition of the limit of a function:

Let $f$ be any function and $a, L\in\mathbb{R}$ real numbers, then we say the limit of $f$ at $a$ is $L$, written as $$ \lim_{x\to a} f(x)=L, $$ if for any given real number $\varepsilon >0$, there exists a positive real number $\delta >0$ such that for any $x\in\mathbb{R}$ satisfying $0<\vert x-a\vert <\delta$, we have $\vert f(x)-L\vert <\epsilon$.

The definition is not easy to understand. In fact, mathematicians spent about two hundred years to rigorously write down the definition of a limit. It was firstly supposed by Newton and finally written down by Weierstrass. In this course we don't quite need to understand this in much detail. This would be done in MATH 425a. Today we'll just see some examples of limits of functions.

We define the Heaviside function to be $$ H(x)=\left\{\begin{array}{ll} 1,&\text{whether}\ x\geq 0;\\ 0,&\text{whether}\ x < 0. \end{array}\right. $$ The graph of this function is shown as below: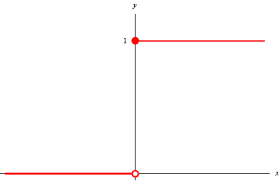

We're caring about the limit $\displaystyle\lim_{x\to 0} H(x)$. Observe from the graph that $H(x)$ has a left-hand limit $0$ at $0$ and right-hand limit $1$ at $0$, which are not the same, so the limit of $H(x)$ does not exist.

Or we can use the precise definition to check if the limit exists. We just need to check for any real number $L$, the limit of $H(x)$ at $0$ is not $L$. To see this, firstly if $L$ is not $0$ and $1$, then for any $x\in\mathbb{R}$, we always have $\vert H(x)-L\vert\geq\min\{\vert L-1\vert ,\vert L\vert\}=\varepsilon_0$ and so for any $\delta >0$, there is a positive real number \varepsilon_0\) so that for any $x$ with $0<\vert x\vert <\delta$, we have $\vert H(x)-L\vert\geq\varepsilon_0$. If $L$ is either $0$ and $1$, then in a small neighbourhood of $0$, we can always find real numbers $x$ so that $H(x)=0$ or $H(x)=1$, so we can just choose $\varepsilon_0 =1$ and then there's always $x$ with $\vert x\vert <\delta $ and $\vert H(x)-L\vert\geq 1$. This tells us that the limit cannot be any real number, so it should not exist.

Now we treat with the homework. Several students asked me about this homework so I think it's worth mentioning.

(Problem 24 in Section 1.3)

Use the graph of $f(x)=x^2$ to find a number $\delta$ such that $$\text{if}\quad \vert x-1\vert <\delta\quad\text{then}\quad\vert x^2-1\vert < \frac{1}{2}$$

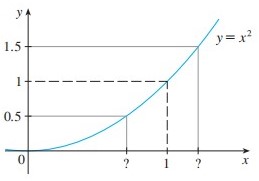
This is a good exercise to help you understand the $\varepsilon$-$\delta$ language. We can divide the solution into two steps: firstly, determine an interval where $x$ lies; secondly, find a $\delta >0$ so that $(1-\delta ,1+\delta )$ is contained in this interval. This $\delta $ is not uniquely determined: any positive real number less than a given number $\delta_0 $ will work.

Calculating Limits

The main idea of calculating limits is to start with standard models and write any such expressions as combinations of essential functions.

Evaluate the limit, if it exists:

$\displaystyle\lim_{\theta\to 0}\frac{\sin (5\theta )}{\theta}$. $\displaystyle\lim_{t\to 0}\frac{\tan 6t}{\sin 2t}$.

For the first problem, we can just use the special limit $\lim_{\theta\to 0}\frac{\sin\theta }{\theta } =1$: $$ \lim_{\theta\to 0}\frac{\sin (5\theta )}{5\theta } =\lim_{\theta\to 0}\frac{5\sin (5\theta )}{5\theta } =5\lim_{\theta\to 0}\frac{\sin (5\theta )}{5\theta }=5\cdot 1=5. $$

For the second one, recall that $\tan 6t=\frac{\sin 6t}{\cos 6t}$, hence we have $f(x)=\frac{\tan 6t}{\sin 2t}=\frac{\sin 6t}{\sin 2t\cos 6t}$. Since $\lim_{t\to 0}\cos 2t=1$, the only problem of this limit is that $\lim_{t\to 0}\sin at=0$ for any real number $a$. To deal with this, we use the special limit $\lim_{t\to 0}\frac{\sin t}{t} =1$ and compute:$$\lim_{t\to 0} f(t)=\lim_{t\to 0}\frac{\sin 6t}{\sin 2t\cos 6t} =\lim_{t\to 0}\frac{\sin 6t}{6t}\frac{2t}{\sin 2t}\frac{6t}{2t\cos 2t} =1\cdot 1\cdot\frac{6}{2} =3.$$

Evaluate the following limit: $$ \lim_{\theta\to 0}\theta^2\sin\frac{1}{\theta}. $$

This does not fit in with any of our previous results, so we should try to use other methods to calculate the limit. Note that the range of $\sin x$ is $[-1,1]$, so we have $-1\leq\sin\frac{1}{\theta }\leq 1$, and hence we get $$-\theta^2\leq\theta^2\sin\frac{1}{\theta }\leq\theta^2.$$Taking the limit at $0$ and apply the squeeze theorem, we get $\lim_{\theta\to 0}\theta^2\sin\frac{1}{\theta } =0$.